直交座標平面上のグラフの方程式を F(x, y) = 0 として、原点を中心にθ回転したとして、その回転させたグラフの方程式がどうなるか考えてみる。
それを考えるために、このグラフ F(x, y) = 0 上の任意の点 Q(s, t) について、これを回転させた点 P(x, y) を考える。
点 Q, P に対応する複素数平面上の点を q = s + ti, p = x + yi とする。
ここで、点 Q をθ回転した点が点 P なので、
p = q(cosθ+i sinθ)
x + yi = (s + ti )(cosθ+i sinθ)
両辺に (cosθ-i sinθ) をかけると、
(x + yi )(cosθ-i sinθ) = s + ti
(xcosθ+ysinθ) + i (-xsinθ+ycosθ) = s + ti
これに対応する座標平面上の点は、
Q(s, t) = (xcosθ+ysinθ, -xsinθ+ycosθ)
ここで、F(x, y) = 0 上の点 Q(s, t) について
F(s, t) = 0 が成り立つので、求めるグラフの方程式は、
F(xcosθ+ysinθ, -xsinθ+ycosθ) = 0
つまり、x を xcosθ+ysinθ、y を -xsinθ+ycosθ で置き換えたものである。
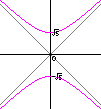
ためしに、双曲線 xy=10 を45°左に回転させたグラフをこの方法で求めてみよう。
x を xcos45°+ysin45°、y を -xsin45°+ycos45°で置き換えると、
(xcos45°+ysin45°)(-xsin45°+ycos45°) = 10
2(x+y)(-x+y) = 10
-x2 + y2 = 5
x2 - y2 = -5
y 軸を軸とする直角双曲線の方程式が導き出せた。