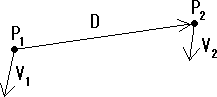
図のように異なる位置ベクトルP1、P2で表される2点が、速度V1、V2で運動しているとき、2点が近付いているか離れてゆくかを調べる。
D=P2-P1とし、t>0、|V1|t≪|D|、|V2|t≪|D|を満たすtを考えたとき、|(P2+V2t)-(P1+V1t)|<|D|であれば近付いている。
この不等式を変形する。
|(P2-P1)+(V2t-V1t)|<|D|
|D+(V2-V1)t|<|D|
両辺とも0より大きいので、
|D+(V2-V1)t|2<|D|2
|D|2+2D・(V2-V1)t+|V2-V1|2t2<|D|2
2D・(V2-V1)+|V2-V1|2t<0
ここで、t→0の極限を取ると、|V2-V1|2tが0または0に限りなく近い正の数であるため、
2D・(V2-V1)<0
D・(V2-V1)<0
従って、D・(V2-V1)<0のとき、2点は近付く。
これは、2点が近付く方向に運動していることを意味している。
同様にして計算すると、離れる条件は、|(P2+V2t)-(P1+V1t)|>|D|から、
2D・(V2-V1)+|V2-V1|2t>0
ここで、t→0の極限を取ると、|V2-V1|2tが0または0に限りなく近い正の数であるため、
D・(V2-V1)>0
または、
D・(V2-V1)=0、かつ、|V2-V1|≠0
前者はお互いに離れる方向に運動していることを意味し、後者は同じ方向に異なる速さで進んでいることを意味している。
最後に、同じ距離を保つ場合を考えると、
|(P2+V2t)-(P1+V1t)|=|D|
2D・(V2-V1)+|V2-V1|2t=0
t>0なので、
D・(V2-V1)=|V2-V1|=0
これは、2点は同じ方向、同じ速さ、すなわち同じ速度で運動していることを意味する。